First Lastname

My awesome biography constrained to a sentence or two goes here.

1 minute read

Integral과 Derivative

Derivative(도함수)가 Function의 순간적인(or 지역적인) 변화율을 나타내는 것과 대조적으로

Integral 은 Function의 전체적인 특성, 어떤 양을 나타냄.

부정적분(Indefinite Integral)

\(F(x)=\int{f(x) dx}\) \(f(x)=\dfrac{d}{dx}F(x)\)

  • 미분의 역연산(anti-derivative = inverse of derivative)
  • 함수의 전체 정의역(domain)에서 정의됨

정적분(definite integral)

리만적분 (Riemann Integral, Limit of Riemann Sum) 으로 근사화하여 구할 수 있음.

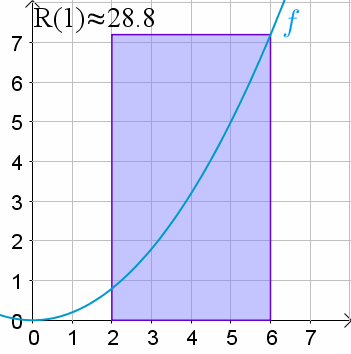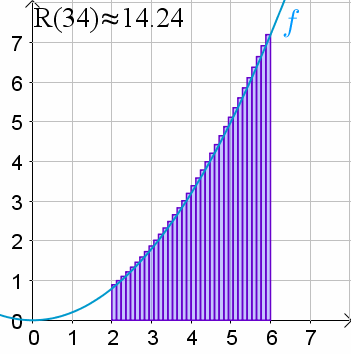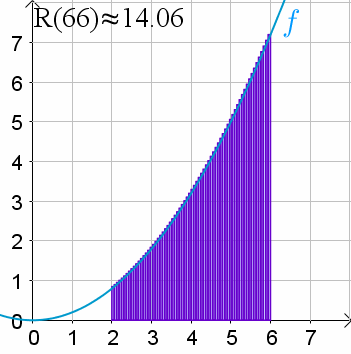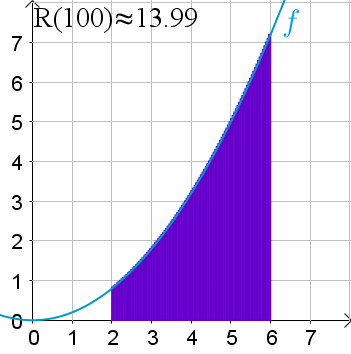
  • 어느 폐구간(closed interval)의 실수값 함수 $f(x)$ 아래의 area를 구함.
  • (무수히 많은 직사각형의) Riemann sum은 definite integral의 근사치를 구하게 해줌.
\[\begin{aligned}R(n)&=\displaystyle \sum^n_{k=1}f(x_k)\Delta x \\&=\sum^n_{k=1}f\left(2+\dfrac{6-2}{n}k\right)\dfrac{6-2}{n}\end{aligned}\]

위의 예에서 Riemann sum은

  • closed interval $[2,6]$에서
  • 각각의 소구간 $[x_{k-1},x_k]$에서
  • 오른쪽 끝점 $x_k=a+k\Delta x$와
  • $\Delta x = (6-2)/n$ 에 대한 것임.
  • 엄밀히는 Riemann의 오른쪽 합임

Riemann sum의 극한으로 구하지 않고도 미적분의 제2기본정리 (The Second Fundamental Theorem of Calculus) 로도 구할 수 있음.

Fundamental Theorem of Calculus

미분과 적분은 서로에 대한 역(inverse)으로 이해할 수 있음.

미적분의 기본정리(Fundamental Theorem of Calculus) 는

  • 어떤 함수를 적분한 후 다시 미분하면 원래의 함수가 되고,
  • 반대로 어떤 함수를 미분한 것을 다시 적분하면 원래의 함수와 같은 형태가 됨을 의미함.

즉, 미분과 적분을 “미적분의 기본정리”가 연결해주고 있음: 각각의 Inverse(역) 으로…

미적분의 제1기본정리

Function $f: [a,b] \rightarrow \mathbb{R}$가 연속인 경우,
function $g: [a,b] \rightarrow \mathbb{R}$을 다음과 같이 정의하자.

\[g(x)=\int^x_af(t)dt\]

이 경우, function $g$는

  • interval $[a,b]$에서 연속이고,
  • $(a,b)$에서 미분가능하며
  • 다음이 성립함.
\[g^\prime(x)=\dfrac{d}{dx}\int^x_af(t)dt=f(x)\]

즉, $g^\prime (x)=f(x)$임.

처음에 주어진 함수 $f$의 정적분을 이용하여
정의한 함수 $g$ ($g$~정적분의 결과)가
바로 $f$의 부정적분들 중 하나 임을 의미.

  • Definite Integral (정적분)이라는 Function의 성질을 규명:
  • 바로 Definite Integral은 Indefinite Integral의 하나임.

미적분의 제2기본정리

Function $f$가 $[a,b]$ 에서 연속이고,
함수 $F$가 $f$의 임의의 indefinite integral function(부정적분)일 때,
다음이 성립함

\[\displaystyle \int^b_a f(x)dx=F(b)-F(a)=\left[F(x)\right]^b_a=\left. F(x) \right|^b_a\]

Definite integral을 “Riemann sum의 극한”으로 구하지않고도 Indefinite Integral에 양 끝점을 대입하여 구하는 방법을 제시.
← indefinite integral로 definite integral을 구함

References

You May Also Enjoy